1. Medir superficies contando baldosas.
2. Unidades de medida de superficie: m2 dm2 cm2 mm2
3. Áreas de algunos polígonos.
4. Área del círculo.
5. Descomponer figuras para hallar su área.
6. Problemas: estudiar casos más sencillos.
1. Medir superficies contando baldosas.
La medida de la superficie de una figura se llama área.
Para aproximar el área de una figura, dibujamos el polígono que más se ajusta a la figura y hallamos su área.
PINCHA EN LAS IMÁGENES PARA PRACTICAR

2. Unidades de medida de superficie: m2 dm2 cm2 mm2
Decímetro cuadrado (dm2). Es la superficie de un cuadrado cuyo lado mide un decímetro.
Centímetro cuadrado (cm2). Es la superficie de un cuadrado cuyo lado mide un centímetro.
Milímetro cuadrado (mm2). Es la superficie de un cuadrado cuyo lado mide un milímetro.
Fíjate solo en las unidades menores que el metro cuadrado.
Pincha en las imágenes para practicar


TEMA 10: LAS FIGURAS PLANAS
1. Los polígonos.
2. Los triángulos.
3. Los cuadriláteros.
4. La circunferencia y el círculo.
5. La longitud de la circunferencia.
6. Problemas: utilizar la regla y el compás.
1. Los polígonos.
Un polígono es una figura plana formada por una línea poligonal cerrada y su interior.
Recuerda que una línea poligonal es una linea formada por segmentos no alineados. Pueden ser abiertas o cerradas
Los elementos de un polígono son:
- Lados: es cada uno de los segmentos que forman la línea poligonal cerrada.
- Vértices: son los puntos donde se unen dos lados consecutivos.
- Ángulos: es la región formada por dos lados consecutivos y el vértice que les une.
- Diagonal: Son los segmentos que unen dos vértices no consecutivos.
Los polígonos según sus lados y sus ángulos pueden ser: regulares o irregulares
Un polígono es regular si todos sus lados son iguales y todos sus ángulos son iguales.
Un polígono es irregular si sus lados y ángulos no son iguales entre sí.
Los polígonos según sus ángulos pueden ser: cóncavos o convexos.
Un polígono es cóncavo si alguno de sus ángulos interiores es cóncavo, es decir, es mayor de 180º y menor de 360º.
Un polígono es convexo si todos sus ángulos interiores son menores de 180º.
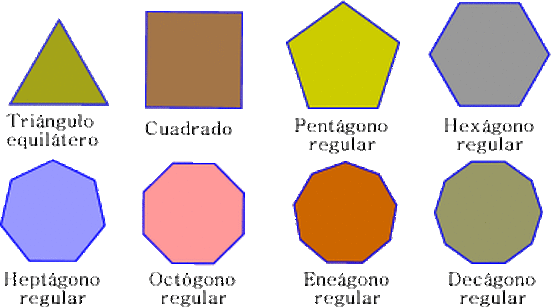
Según su número de lados, los polígonos pueden ser:
El perímetro de un polígono es la suma de las longitudes de todos sus lados.
El perímetro de un polígono regular es la suma de todos sus lados. Como todo polígono regular tiene todos sus lados iguales, el perímetro será el producto del número de lados del polígono por la longitud de uno de ellos.
Un polígono irregular tiene alguno o todos sus lados diferentes. Por lo tanto, el perímetro del polígono irregular es la suma de todos sus lados.
PINCHA EN LAS IMÁGENES PARA PRACTICAR.





2. Los triángulos.
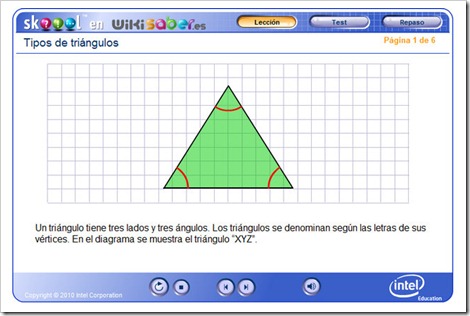
Los triángulos son polígonos de 3 lados, 3 vértices, 3 ángulos y ninguna diagonal.
Sus ángulos interiores suman 180º.
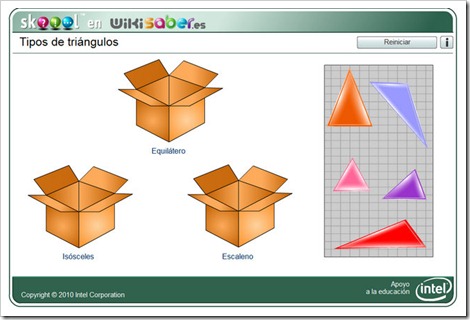
Los triángulos se pueden clasificar según sus lados en:
1. Triángulo equilátero: tiene los 3 lados iguales.
2. Triángulo isósceles: tiene 2 lados iguales.
3. Triángulo escaleno: no tiene ningún lado igual.
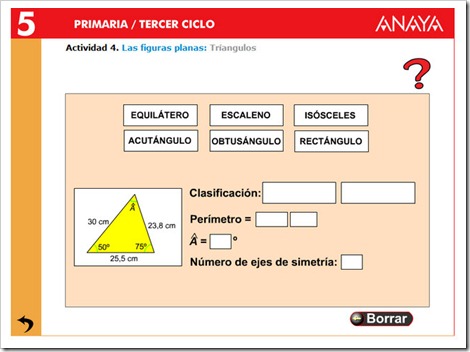
Los triángulos se pueden clasificar según sus ángulos en:
1. Triángulo rectángulo: tienen un ángulo recto.
En u n triángulo rectángulo, los lados reciben un nombre especial. Los lados que forman el ángulo de 90º se llaman catetos, y el otro lado, se llama hipotenusa.
2. Triángulo obtusángulo: tiene un ángulo obtuso.
3. Triángulo acutángulo: tiene los 3 ángulos agudos.
FÍJATE EN ESTA IMAGEN.
PINCHA EN LAS IMÁGENES PARA PRACTICAR



3. Los cuadriláteros.
Los cuadriláteros son polígonos que tienen 4 lados, 4 vértices, 4 ángulos y 2 diagonales.
Sus ángulos interiores suman 360º.
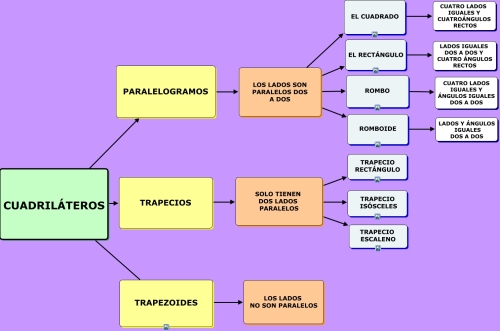
Los polígonos cuadriláteros se clasifican en:
1. Cuadriláteros paralelogramos: son aquellos que tienen los lados paralelos 2 a 2.
Son cuadriláteros paralelogramos:
- cuadrado: tiene los 4 lados iguales y los 4 ángulos iguales (90º)
- Rectángulo: tiene los lados iguales 2 a 2 y los 4 ángulos iguales (90º)
- Rombo: tiene los 4 lados iguales y los ángulos iguales 2 a 2.
- Romboide: tiene los lados iguales 2 a 2 y los ángulos iguales 2 a 2.
2. Cuadriláteros no paralelogramos: son aquellos cuadriláteros que sólo tienen dos lados paralelos o ningún lado paralelo a otro.
Los cuadriláteros no paralelogramos son:
- Trapecio: tiene dos lados paralelos
- Trapezoide: no tiene ningún lado paralelo.
Podemos distinguir tres clases de Trapecios, que son:
PINCHA EN LAS IMÁGENES PARA PRACTICAR


TRIVIAL
4. La circunferencia y el círculo.
La circunferencia es una línea curva cerrada y plana que todos sus puntos equidistan de un punto llamado centro.
El círculo es una figura plana formada por una circunferencia y su interior.
Los elementos de una circunferencia son:
- centro: es el punto que equidista (tiene la misma distancia) de cualquier punto de la circunferencia.
- radio: segmento que va desde el centro a cualquier punto de la circunferencia.
- diámetro: segmento que va de un punto a otro de la circunferencia pero pasando por el centro.
- cuerda: segmento que va de un punto a otro de la circunferencia. La cuerda de mayor longitud es el diámetro.
- arco: trozo de circunferencia que está delimitada por una cuerda. Recuerda: cuando dibujamos una cuerda siempre escogemos el arco más pequeño de los dos en los que se divide la circunferencia.
- Semicircunferencia: mitad de la circunferencia.
Los elementos de un círculo son:

zona circular: porción del círculo limitada por dos cuerdas.
Exterior: si la recta y la circunferencia no tienen ningún punto en común.
Tangente: si la recta y la circunferencia sólo tienen un punto en común.
Secante: si la recta y la circunferencia tienen dos puntos en común.
PINCHA EN LAS IMÁGENES PARA PRACTICAR


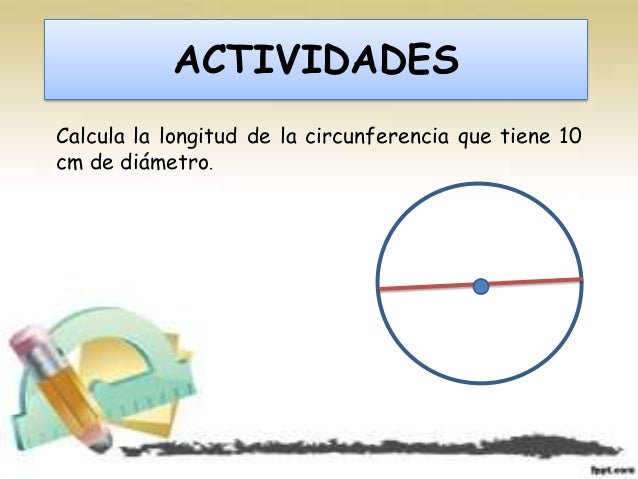
5. La longitud de la circunferencia.
Calculamos la longitud de una circunferencia al multiplicar el diámetro de la circunferencia ( o 2 veces su radio, recuerda que el Diámetro = 2 x radio) por una constante que es la letra griega pi .

Su valor se aproxima, 3, 14
PINCHA EN LAS IMÁGENES PARA PRACTICAR
TEMA 9: ÁNGULOS
1. Ángulos y su medida .
2. Clasificación de ángulos.
3. Operar con grados, minutos y segundos.
4. Mediatriz de un segmento y bisectriz de un ángulo.
5. Simetría y traslaciones.
6. Posición en el plano. Movimientos.
7. Problemas: paso a paso con un dibujo.
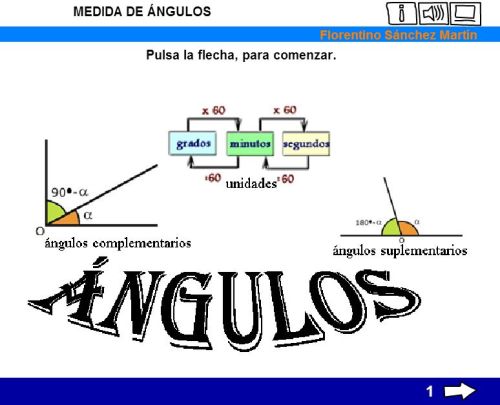
Un ángulo es la región comprendida entre dos semirrectas (lados) que se cortan en un punto, llamado vértice.
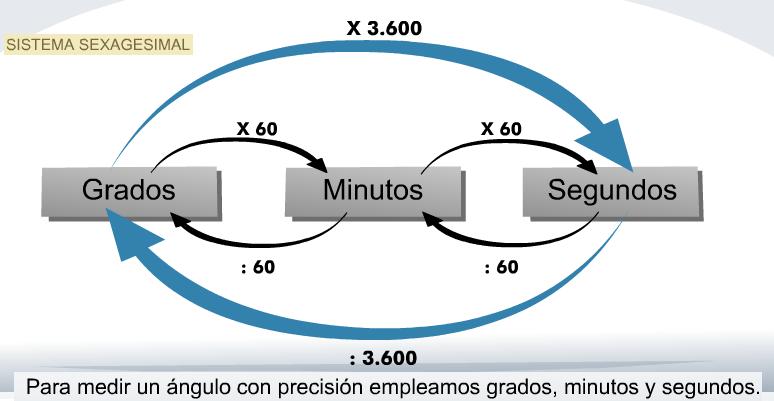
Para medir ángulos utilizamos grados (º), minutos (’) y segundos (’’). Estas unidades forman parte del sistema sexagesimal, pues para pasar de unas a otras multiplicamos o dividimos por 60.
1 minuto = 60 segundos
1 grado = 3.600 segundos
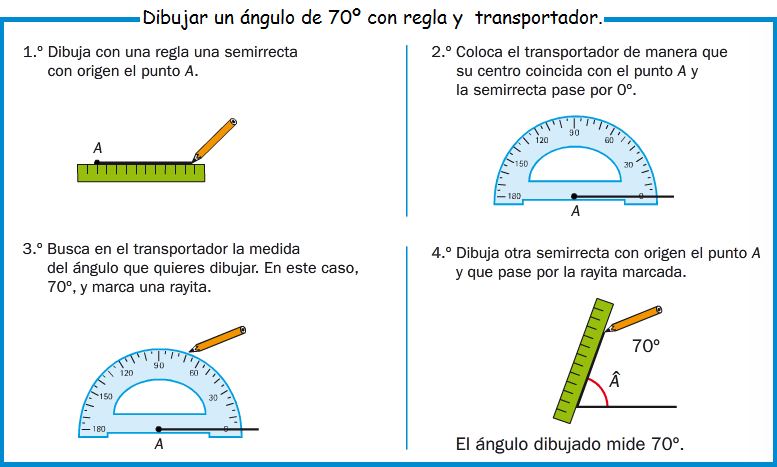
PINCHA EN LA IMAGEN PARA PRACTICAR





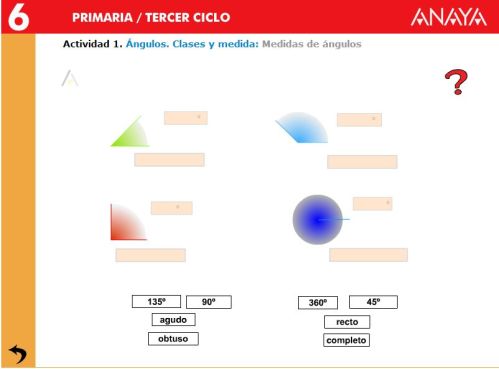
2. Clasificación de ángulos.
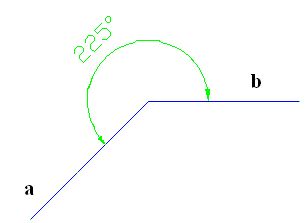
Pero ¿cómo se llama el ángulo que mide más de 180º y menos de 360º?
Es el ángulo entrante o cóncavo. > 180º < 360º
OBSERVA ESTE VÍDEO: TE EXPLICA PASO A PASO CÓMO PUEDES MEDIR UN ÁNGULO CÓNCAVO.
PINCHA EN LAS IMÁGENES PARA PRACTICAR
CALCULAMOS EL COMPLEMENTARIO O SUPLEMENTARIO DE UN ÁNGULO.







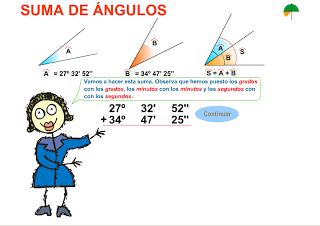
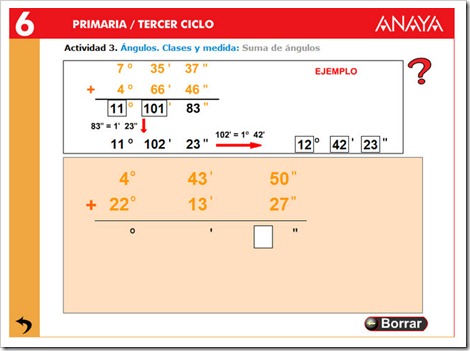
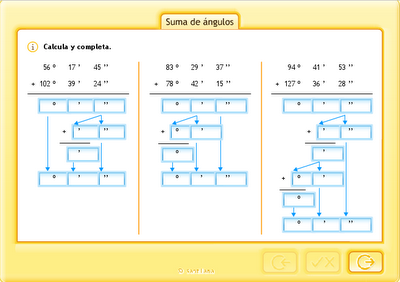
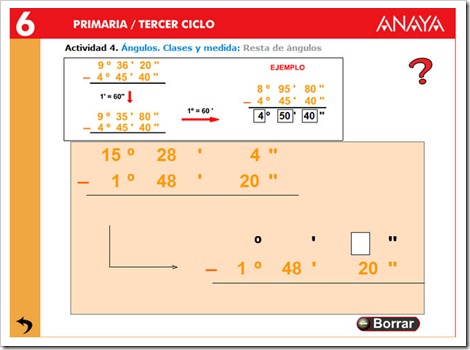
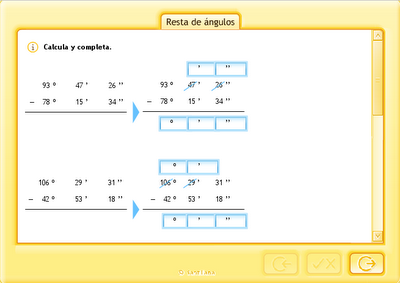
3. Operar con grados, minutos y segundos.
OBSERVA ESTOS VÍDEOS
PINCHA EN LAS IMÁGENES PARA PRACTICAR

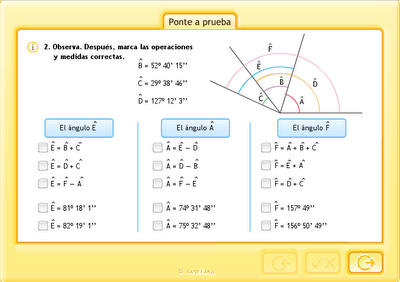
4. Mediatriz de un segmento y bisectriz de un ángulo.
OBSERVA EL VÍDEO : TRAZAR UNA MEDIATRIZ
La mediatriz de un segmento es una recta perpendicular al segmento que pasa por su punto medio.
OBSERVA EL VÍDEO: TRAZAR UNA BISECTRIZ.
La bisectriz de un ángulo es una semirrecta que pasa por el vértice del ángulo y lo divide en dos partes iguales.
5. Simetría y traslaciones.
PINCHA EN LAS IMÁGENES PARA PRACTICAR




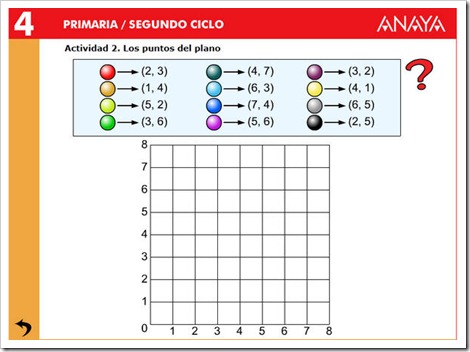
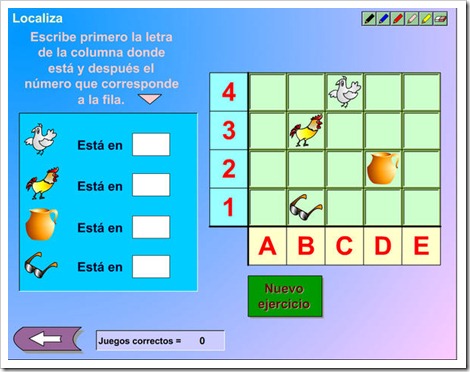
6. Posición en el plano. Movimientos.
Para representar puntos en el plano se utiliza el sistema de coordenadas cartesianas.
Cualquier punto del plano se representa mediante dos números que llamamos coordenadas.
Las coordenadas cartesianas nos permiten representar y localizar puntos en un plano de forma sencilla.
El eje vertical es el eje Y o eje de las ordenadas.
PINCHA EN LA IMAGEN PARA PRACTICAR


TEMA 8: MEDIR EL TIEMPO Y EL DINERO
ÍNDICE:
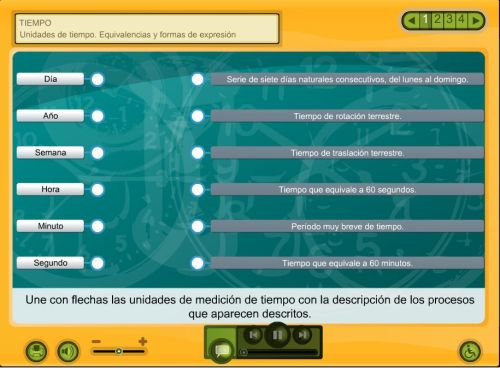
1. Unidades de tiempo menores y mayores que el año
2. Periodos de tiempo menores que el día: horas, minutos y segundos.
3. Distintos modos de expresar medidas de tiempo.
4. Sumar y restar datos de tiempo.
5. Monedas y billetes. Operaciones.
6. Problemas: responder preguntas intermedias.
1. Unidades de tiempo menores y mayores que el año
Unidades mayores que el año
Bienio = 2 años
trienio = 3 años
Cuatrienio = 4 años
Lustro o quinquenio = 5 años
Sexenio = 6 años
Septenio = 7 años .....
Unidades menores que el año
semana = 7 días
quincena = 15 días
mes = 28, 29, 30 o 31 días.
Trimestre = 3 meses
Cuatrimestre = 4 meses
Semestre = 6 meses ...
Calculamos a qué siglo pertenece un año.

Recuerda: año 1 al 99 = siglo I
si eliminamos la unidades y decenas, no queda nada: 0 + 1 = 1
PINCHA EN LAS IMÁGENES PARA PRACTICAR


2. Periodos de tiempo menores que el día: horas, minutos y segundos.
1 hora = 60 x 60 = 3600 s
1 día = 24 x 60 x 60 = 86. 400 s
1/2 h = 30 min = 1.800 s
1/4 h = 15 min = 900 s
Para pasar de unas unidades de tiempo a otras se multiplica o divide por 60, por eso el sistema de unidades de tiempo se llama sistema sexagesimal.
1 h = 60 min
1 min = 60 s
1 h = 3.600 s
ESTOS VÍDEOS TE PUEDEN RESULTAR INTERESANTES
PINCHA EN LAS IMÁGENES PARA PRACTICAR
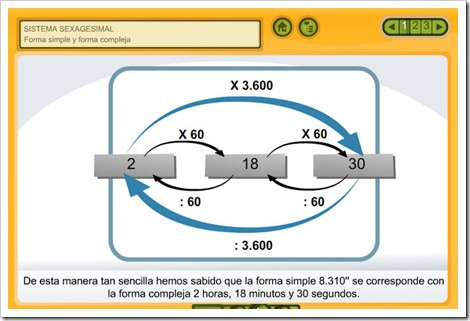


3. Distintos modos de expresar medidas de tiempo.
El cronómetro de Manuel señala que su madre ha tardado 7.692 s en llegar a la meta. Sin embargo, el reloj de la carrera marca 2 h 8 min 12 s.
| expresión incompleja (una sola unidad) | expresión compleja (dos o más unidades) |
|---|---|
| 7.692 s | 2 h 8 min 12 s |
7. 692 S = 2 h 8 min 12 s
Una medida de tiempo está expresada en forma incompleja cuando se utiliza una sola unidad, y en forma compleja, cuando se utilizan dos o más unidades.
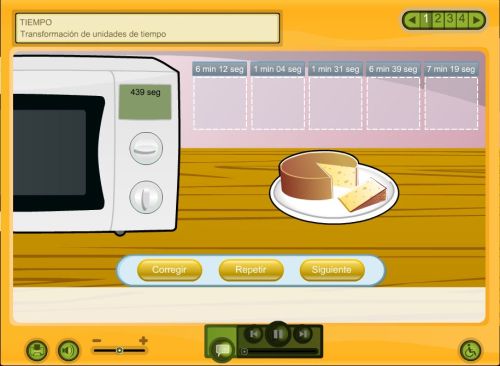

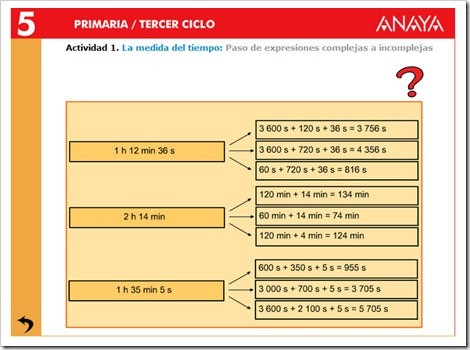
4. Sumar y restar datos de tiempo.
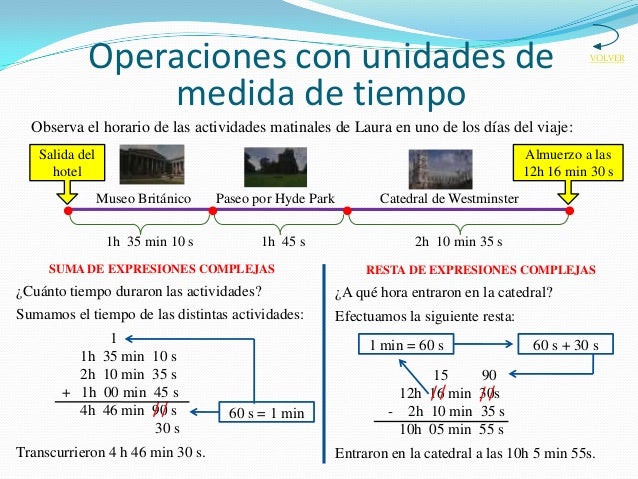





Repaso de unidades de medida











5. Monedas y billetes. Operaciones.
El euro es la unidad monetaria de la Unión Europea, su símbolo es €. Cada euro se divide en 100 partes iguales, llamadas céntimos y se escribe cent.
PINCHA EN LA IMAGEN PARA PRACTICAR





6. Problemas: responder preguntas intermedias.
Lee este problema (es el que tienes en tu libro como ejemplo)
En el instituto Julio tiene 3 clases al día de 55 min y 3 de 45 min. Si a media mañana descansa 24 min, ¿cuántas horas a la semana pasa en el instituto?

- ¿Qué nos pide el problema?
Averiguar cuántas horas semanales pasa Julio en el instituto. - ¿Qué datos necesitamos?
– Las clases que tiene en un día y su duración: 3 clases de 55 min y 3 clases de 45 min.
– El tiempo de descanso diario: 24 min. - ¿Cómo se resuelve?
- Pensamos qué preguntas intermedias podemos plantear y las resolvemos.1º. ¿Cuántas horas pasa Julio en clase cada día?55 × 3= 165 45 × 3 = 135 y sumamos los resultados 135 + 165 = 300 después convertimos los 300 minutos que pasa Julio al día en clase en horas (: 60) 300 : 60 = 5Pasa 300 min en clase cada día, que son 5 h.2º. ¿Y a la semana? solo va 5 días a clase (de lunes a viernes)5 × 5 = 25Pasa 25 h en clase a la semana.3º. ¿Cuántas horas de descanso tiene a la semana?24 min en un día, pues en 5 días 24 × 5 = 120 Paso los minutos a horas (: 60) 120 : 60 = 2Tiene 2 h de descanso semanales.4º. ¿Cuántas horas a la semana pasa Julio en el instituto?ahora suma las horas que pasa en clase a la semana y las de descanso 25 + 2 = 27
Solución
Julio pasa 27 h semanales en el instituto.
TEMA 5: NÚMEROS DECIMALES
1. Números decimales.
2. Comparar y representar números decimales.
3. Redondear números decimales.
4. Comparar números.
5. Problemas: localizar los datos necesarios.
1. Números decimales.
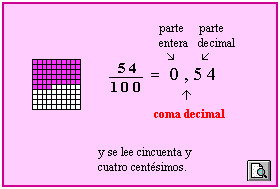
Un número decimal tiene dos partes separadas por una coma. La parte entera está delante de la coma y la parte decimal está detrás de la coma.
Los números decimales se pueden leer de dos formas:
- Se lee el número de la parte entera, se dice coma y después se lee el número de la parte decimal.
Ejemplo 3, 14 : tres coma catorce.
¡Cuidado! Si hay ceros detrás de la coma, antes de cualquier otro número, debemos decirlo.
Ejemplo: 3, 014: tres coma cero catorce.
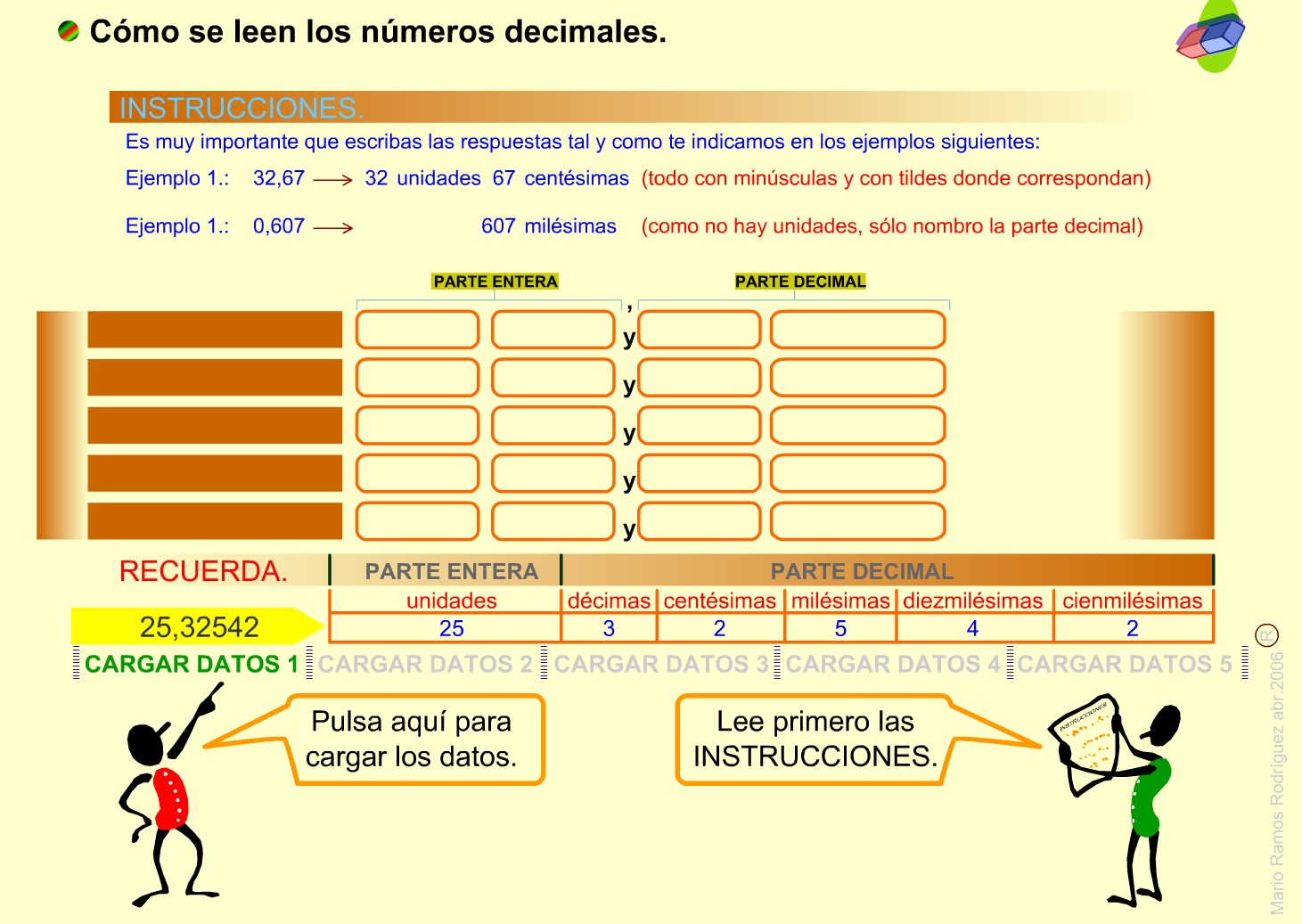
- También se pueden leer los números decimales, diciendo el número de unidades que hay y después el número decimal con su unidad correspondiente.
Ejemplo:3, 14 : tres unidades y catorce centésimas (porque la cifra 4, que es el último decimal, ocupa la posición de las centésimas).
3, 014: tres unidades y 14 milésimas (porque la cifra 4, que es el último decimal, ocupa la posición de las milésimas)
PRACTICA PINCHANDO EN LAS IMÁGENES



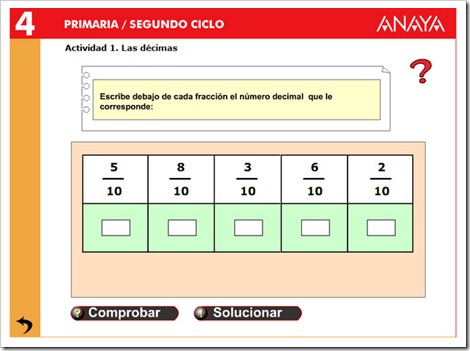
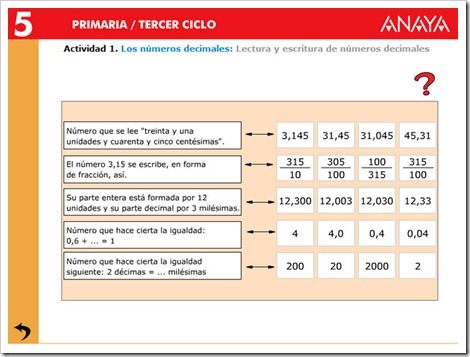
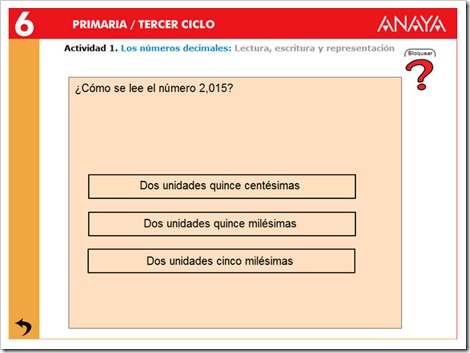
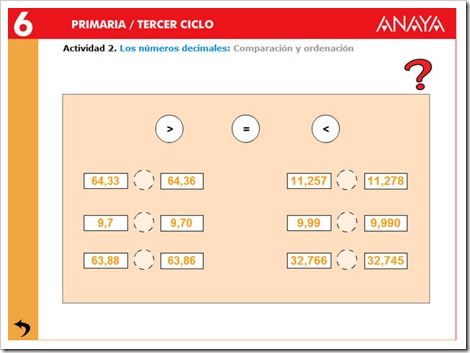
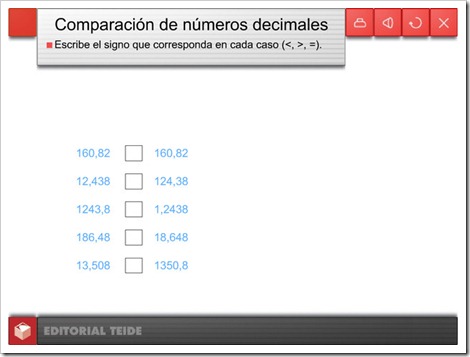
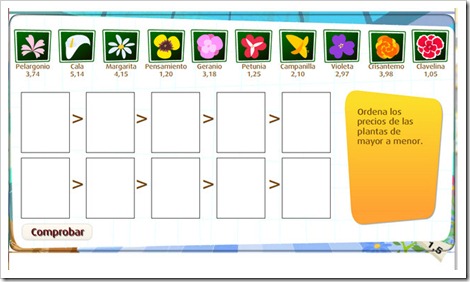
2. Comparar y representar números decimales.

Para comparar dos números decimales primero debemos comparar la parte entera:
Ejemplo: 1, 323 y 1, 435
Como tienen la misma parte entera, pasamos a comparar la parte decimal, y empezamos por las décimas.
1, 323 tiene 3 décimas y 1, 435 tiene 4 décimas.
El segundo número tiene más décimas, por lo que
1, 435 > 1, 323
PRACTICA PINCHANDO EN LAS IMÁGENES
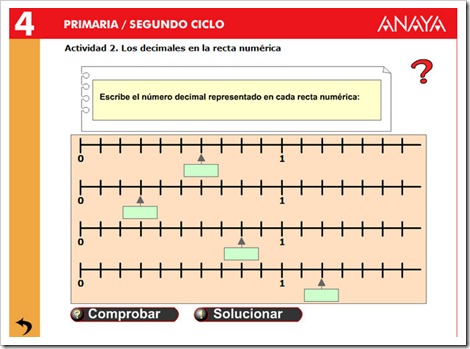
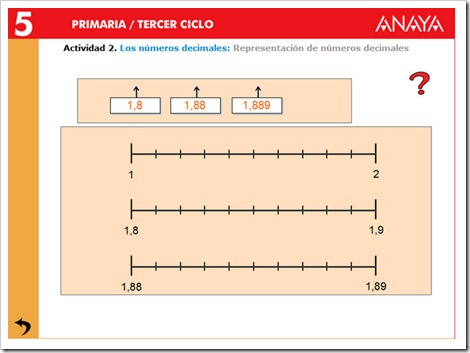
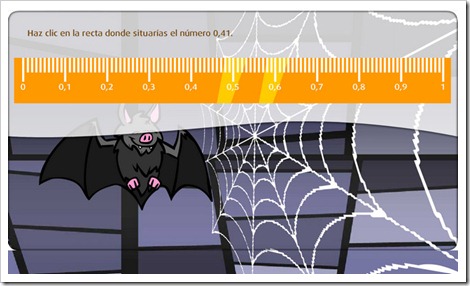



3. Redondear números decimales.
- Podemos redondear un número decimal utilizando la recta numérica. Miramos entre qué unidades, décimas o centésimas se encuentra, y tomamos la más cercana.
1,29 está comprendido entre 1 y 2. La unidad más próxima es 1.
1,29 está comprendido entre 1,2 y 1,3. La décima más próxima es 1,3.
- También podemos fijarnos en sus cifras.
Para redondear a la unidad, nos fijamos en la cifra de las décimas.
- Si es menor que 5, dejamos las unidades igual.
- Si es igual o mayor que 5, sumamos 1 a las unidades.
Para redondear a la décima, nos fijamos en la cifra de las centésimas.
- Si es menor que 5, dejamos las décimas igual.
- Si es igual o mayor que 5, sumamos 1 a las décimas.
Para redondear a la centésima, nos fijamos en la cifra de las milésimas.
- Si es menor que 5, dejamos las centésimas igual.
- Si es igual o mayor que 5, sumamos 1 a las centésimas.
PINCHA EN ESTAS IMÁGENES PARA PRACTICAR




4. Comparar números.
Para comparar números, representamos cada cantidad en la recta numérica. Para ello, primero vemos cómo están escritos: fracciones y números decimales.

5. Problemas: localizar los datos necesarios.
PRACTICA PINCHANDO EN LA IMAGEN

----------------------------------------------
Tema 4: operar con fracciones
1. Sumar fracciones.
2. Restar fracciones.
3. La fracción como división.
4. Porcentajes.
5. Porcentaje de una cantidad.
6. Problemas: utilizar el dibujo.
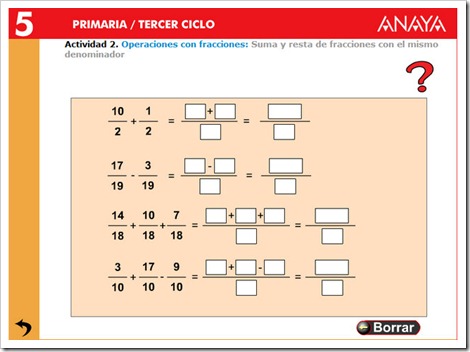
1. Sumar fracciones.
Para sumar fracciones con el mismo denominador, dejamos el mismo denominador y sumamos los numeradores.
Para calcular 2/ 4 + 1/ 2 , buscamos que tengan el mismo denominador calculando fracciones equivalentes.
Como 2/4 y 2/4 tienen el mismo denominador, podemos sumarlas:
Para sumar fracciones con distinto denominador, buscamos fracciones equivalentes con el mismo denominador y sumamos los numeradores.
2. Restar fracciones.
Para restar fracciones con el mismo denominador, dejamos el mismo denominador y restamos los numeradores.
Para restar fracciones con distinto denominador, buscamos fracciones equivalentes con el mismo denominador y restamos los numeradores.
PRACTICA

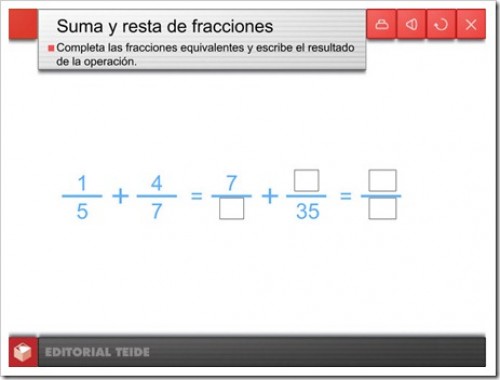
3. La fracción como división.

25 : 5 = 5 Y NO SOBRA NADA

Al hacer la división obtenemos un número entero (el cociente) y otro que no se puede repartir (resto). Recuerda que el resto es una fracción que tiene como numerador el número del resto y como denominador el divisor.
OBSERVA EL VÍDEO
Practica el número mixto
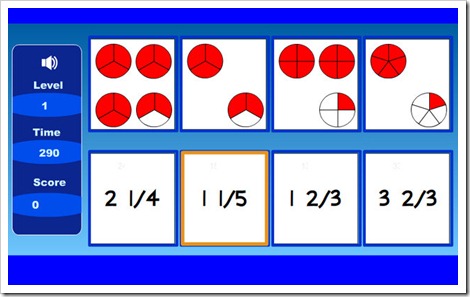
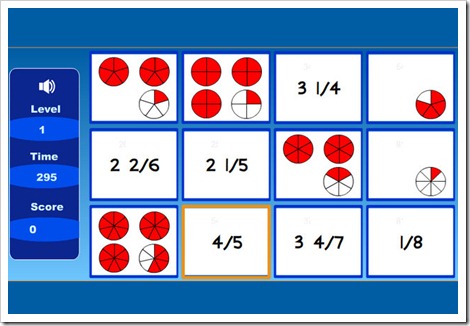
4. Porcentajes.
5. Porcentaje de una cantidad.
PRACTICA PINCHANDO EN LAS IMÁGENES



TEMA 3: LAS FRACCIONES
1. Elementos de una fracción.
2. Fracciones equivalentes.
3. Comparar fracciones.
4. Fracciones de una cantidad.
5. Problemas: representar gráficamente el problema.
1. Elementos de una fracción.
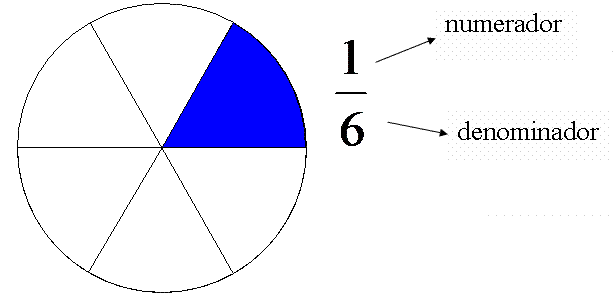
Los elementos de una fracción son:
numerador: partes que cogemos
denominador:partes iguales en las que dividimos la unidad.
Si el numerador es menor que el denominador, la fracción es menor que la unidad y se llama propia.
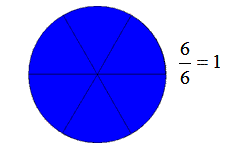
Si el numerador es igual que el denominador, la fracción es igual a la unidad.
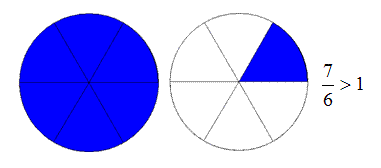
Si el numerador es mayor que el denominador, la fracción es mayor que la unidad y se llama impropia.

2. Fracciones equivalentes.
Dos fracciones son equivalentes cuando representan la misma parte de la unidad.
Para comprobar si dos fracciones son equivalentes, multiplicamos los términos en cruz.

Podemos calcular fracciones equivalentes de dos formas.
- Dividimos el numerador y el denominador por el mismo número.
- Multiplicamos el numerador y el denominador por el mismo número.

Una fracción es irreducible cuando no podemos dividir su numerador y denominador por un mismo número.
PRACTICA

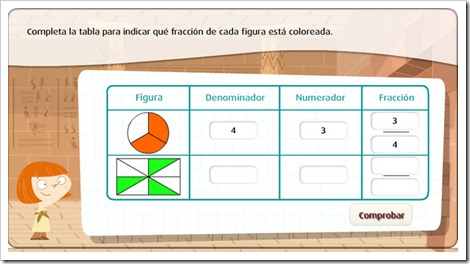


PARA OBTENER LA FRACCIÓN IRREDUCIBLE:
33
----
21
Buscamos todos los divisores del numerador y el denominador.
33: 1, 3, 11, 33
21: 1, 3, 7, 21
Nos quedamos con los divisores que son iguales en ambos números: 1 y 3
Nos quedamos con el más grande: 3
Dividimos numerador y denominador por ese número
33 : 3 11
----- = ---------
21 : 3 7
11
------- es la fracción irreducible.
7


3. Comparar fracciones.
A la hora de comparar fracciones nos podemos encontrar con tres situaciones:
1º Que las fracciones que comparo tengan el mismo denominador:
Es mayor aquella que tenga el numerador mayor.
2º Que las fracciones tengan el mismo numerador.
Es mayor la que tiene el denominador más pequeño.
3º Que tengan distinto numerador y denominador.
--------- ? --------
6 8
Debo buscar una fracción equivalente de las dos que tengan el mismo denominador. En este caso busco en la tabla del 6 y del 8
y observamos cual es el primer múltiplo que comparten: el 24
Busco las fracciones equivalentes de 1/8 y 1/ 6 que tengan como denominador 24
1/6 (debo multiplicar a 6 x 4 para que me dé 24, así que debo multiplicar a su numerador también por 4)
2 8
---- = ------
6 24
1/8 (debo multiplicar a 8 x 3 para que me dé 24, así que debo multiplicar a su numerador también por 3)
1 3
------- = --------
8 24
Al tener el mismo denominador, les puedo comparar. Es mayor el que tenga el numerador mayor.
8 3 2 1
------- > ------- por lo que ------ > ------
24 24 6 8
4. Fracciones de una cantidad.
Para calcular la fracción de una cantidad, dividimos la cantidad entre el denominador y multiplicamos el resultado por el numerador.

--------------------------------------------------------------------------------
TEMA 2: MÚLTIPLOS Y DIVISORES
1. Múltiplos de un número.
2. Divisores de un número.
3. Criterios de divisibilidad.
4. Números primos y compuestos.
5. Problemas: descubrir la secuencia lógica mediante una tabla.
1. MÚLTIPLOS DE UN NÚMERO.
Los múltiplos de un número se obtienen al multiplicar ese número por los números naturales.
Para comprobar si un número es múltiplo de otro, se divide el primero entre el segundo y la división debe ser exacta.
52 es múltiplo de 7 ?
52 : 7 = 7 Resto es 3 . Por eso 52 no es múltiplo de 7.
42 es múltiplo de 7?
42 : 7 = 6 Resto es 0. Por eso 42 es múltiplo de 7
¡¡¡PRACTICA PINCHANDO EN ESTAS IMÁGENES!!!



TAMBIÉN PUEDES OBSERVAR ESTE VÍDEO
2. DIVISORES DE UN NÚMERO.
Un número es divisor de otro si al hacer la división el resto es cero. Para calcular los divisores de un número, lo dividimos entre los números naturales: 1, 2, 3… menores o iguales que él.
Todo número es divisible por 1
El mayor divisor de un número es el propio número
OBSERVA ESTE VÍDEO
PRACTICA PINCHANDO EN ESTAS ACTIVIDADES




3. CRITERIOS DE DIVISIBILIDAD.
PRACTICA PINCHANDO EN LAS IMÁGENES
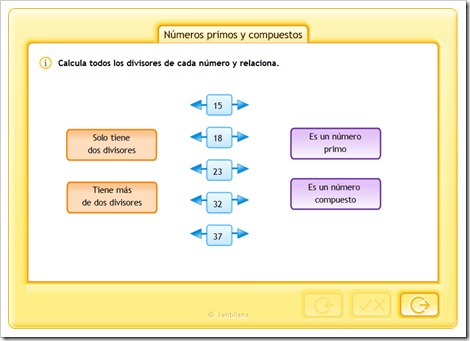
4. NÚMEROS PRIMOS Y COMPUESTOS.
El 0 y el 1 son dos números especiales, no son ni números primos, ni números compuestos.
Un número es primo si solo tiene dos divisores, él mismo y la unidad.
Un número es compuesto si tiene más divisores que él mismo y la unidad.
NÚMEROS PRIMOS HASTA EL 100.
Pincha en la tabla y verás cómo se obtienen.
Te lo explico otra vez. Pincha en la imagen.

Pincha en la imagen para practicar


-----------------------------------------------------------------------
TEMA 1: LOS NÚMEROS NATURALES
1. Sumar y restar.
2. Multiplicar y dividir.
3. Jerarquía de operaciones.
4. Las potencias: cuadrados y cubos.
5. Potencias de base 10.
6. Problemas: resolver paso a paso.
Un número natural es el que sirve para designar la cantidad de elementos que tiene un conjunto (número cardinal: 1, 2, 3, 4, 5, 6,...) o para indicar el orden o posición de un elemento en un conjunto (número ordinal: 1º, 2º, 3º, 4º, 5º, ...).
Los números naturales son ilimitados.
Nuestro sistema de numeración es decimal, es decir, que un conjunto de 10 unidades nos lleva al siguiente orden: la decena; 10 decenas nos lleva al siguiente orden: la centena; 10 centenas nos llevan al siguiente orden: la unidad de millar y así sucesivamente.
Nuestro sistema de numeración es:
1. Sistema decimal
Para representar números mayores que nueve, se agrupan los elementos de 10 en 10 para formar una unidad del orden inmediato superior.
2. Sistema posicional
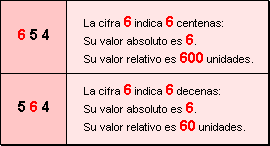
Por lo tanto, la posición de cada cifra, a medida que nos trasladamos de derecha a izquierda, nos indicará el valor relativo de la misma. Por ello se dice que es un sistema posicional.
El valor relativo de una cifra depende del lugar que ocupe dentro de un número.
La prueba de la división:
Dividendo = divisor x cociente + resto
4 x 3 + 2 = 14 4 x 3 + 0 = 12
La prueba del resto:
El resto de una división debe ser siempre menor que el divisor.
La propiedad fundamental de la división:
Si el dividendo y el divisor de una división se multiplican o se dividen por el mismo número, el cociente no varía, pero el resto queda multiplicado o dividido por ese número.
Estas dos divisiones son equivalentes. 85: 9 = 9 resto = 4
170 : 18 = 9 resto = 8
El cociente no varía, es 9
85 x 2 = 170
4 x 2 = 8
3.- JERARQUÍA DE OPERACIONES
4.- LAS POTENCIAS: CUADRADOS Y CUBOS

Un número natural es el que sirve para designar la cantidad de elementos que tiene un conjunto (número cardinal: 1, 2, 3, 4, 5, 6,...) o para indicar el orden o posición de un elemento en un conjunto (número ordinal: 1º, 2º, 3º, 4º, 5º, ...).
Los números naturales son ilimitados.
Nuestro sistema de numeración es decimal, es decir, que un conjunto de 10 unidades nos lleva al siguiente orden: la decena; 10 decenas nos lleva al siguiente orden: la centena; 10 centenas nos llevan al siguiente orden: la unidad de millar y así sucesivamente.
Nuestro sistema de numeración es:
1. Sistema decimal
Para representar números mayores que nueve, se agrupan los elementos de 10 en 10 para formar una unidad del orden inmediato superior.
2. Sistema posicional
Por lo tanto, la posición de cada cifra, a medida que nos trasladamos de derecha a izquierda, nos indicará el valor relativo de la misma. Por ello se dice que es un sistema posicional.
1.- SUMAR Y RESTAR
1.1.- SUMAR
Los términos de la suma son: sumandos y suma o total.
1.1.- SUMAR
Los términos de la suma son: sumandos y suma o total.
La suma tiene dos propiedades:
1. Propiedad conmutativa: cuando sumamos dos sumandos, su orden no altera el resultado.
4 + 5 = 5 + 4
2. Propiedad asociativa: cuando sumamos tres sumandos, obtenemos el mismo resultado si sumamos primero el 1º y el 2º y después el 3º sumando, que si sumamos el 2º y 3º sumando y por último el 1º.
(2+4)+5= 2+(4+5)
1.2.- RESTAR
Los términos de la resta son: minuendo (número mayor), sustraendo y diferencia.
La resta no tiene propiedad conmutativa ni asociativa.
1.3.- REDONDEO
Redondear a la centena:
1. 471 ---- está entre el 1.400 y el 1.500
Si es menor que 4, cogemos el menor.
Si es igual o mayor de 5, cogemos el mayor.
Como 7 es mayor que 5, nos quedamos con el mayor: 1.500
2.- MULTIPLICAR Y DIVIDIR
2.1.- MULTIPLICAR
Los términos de la multiplicación son: los factores y el producto.
La multiplicación tiene propiedades:
1. Propiedad conmutativa: cuando multiplicamos dos factores, su orden no altera el producto.
12 x 3 = 3 x 12 = 36
2. Propiedad asociativa: cuando multiplicamos tres factores, obtenemos el mismo resultado si multiplicamos primero el 1º y el 2º y después el 3º factor, que si multiplicamos el 2º y 3º factor y por último el 1º.
(5 × 7) × 11 = 5 × (7 × 11) = 385
3. Propiedad distributiva:la multiplicación de un número por
una suma es igual a la suma de las multiplicaciones de dicho
número por cada uno de los sumandos.
239 x (100 + 20 + 5) = 239 x100 + 239 x 20 + 239 x 5 =
29875
2.2.- DIVIDIR
Los términos de la división son: dividendo, divisor, cociente y resto.
Podemos encontrarnos con dos tipos de divisiones:
- Una división es exacta cuando el resto es cero.
- Una división es entera cuando el resto es distinto de cero.
La prueba de la división:
Dividendo = divisor x cociente + resto
4 x 3 + 2 = 14 4 x 3 + 0 = 12
La prueba del resto:
El resto de una división debe ser siempre menor que el divisor.
La propiedad fundamental de la división:
Si el dividendo y el divisor de una división se multiplican o se dividen por el mismo número, el cociente no varía, pero el resto queda multiplicado o dividido por ese número.
Estas dos divisiones son equivalentes. 85: 9 = 9 resto = 4
170 : 18 = 9 resto = 8
El cociente no varía, es 9
85 x 2 = 170
4 x 2 = 8
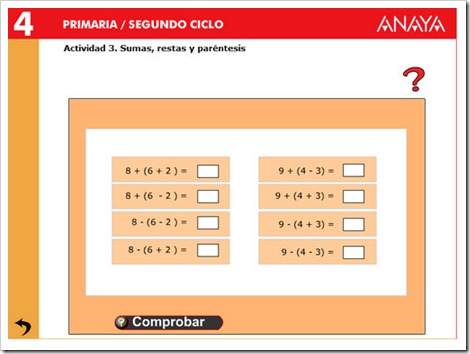
3.- JERARQUÍA DE OPERACIONES
En una expresión con varias operaciones:
1.º
Si hay paréntesis, resolvemos primero las operaciones que están dentro de los paréntesis.
2.º
Resolvemos las multiplicaciones y divisiones de izquierda a derecha.
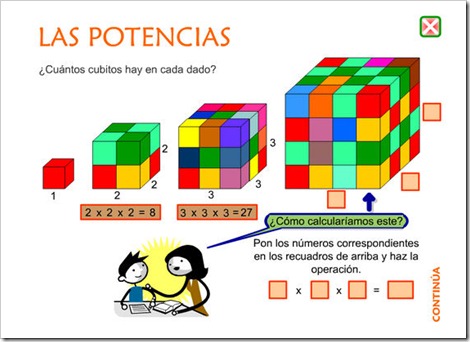
Un producto de factores iguales se puede escribir en forma de potencia.
5 × 5 × 5 × 5 = 54
54 es una potencia. Se lee cinco elevado a cuatro.

Multiplicar dos veces el mismo número, es hallar el cuadrado de ese número.
42 = 4 × 4
Se lee cuatro elevado a dos o cuatro elevado al cuadrado.
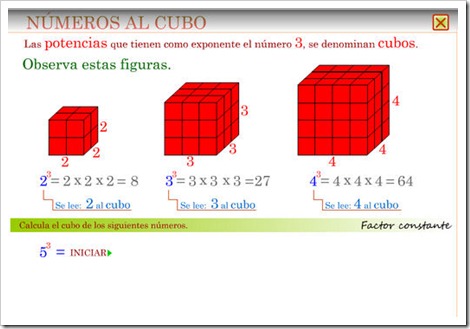
Multiplicar tres veces el mismo número, es hallar el cubo de ese número.
43 = 4 × 4 × 4
Se lee cuatro elevado a tres o cuatro elevado al cubo.
- Cualquier potencia, cuya base sea cualquier número y este elevada a 0, es 1
50 = 1
60 = 1
120 = 1
330 = 1
- Cualquier potencia, cuya base sea cualquier número y este elevada a 1, es ese número.
61 = 6
121 = 12
331 = 33
AHORA, PRACTICA PINCHANDO EN ESTAS ACTIVIDADES
5.- POTENCIAS DE BASE 10
Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente.
Cualquier número se puede expresar como una suma de cifras por potencias de base 10. Es la expresión polinómica de un número.
3.456 = 3.000 + 400 + 50 + 6 = 3 x 103 + 4 x 102 + 5 x 10 + 6
AHORA, PRACTICA PINCHANDO EN ESTAS ACTIVIDADES
Una potencia de base 10 es igual a la unidad seguida de tantos ceros como indica el exponente.
| 1.392.000 = | 1.000.000 | + | 300.000 | + | 90.000 | + | 2.000 = |
| 1 x 106 | + | 3 × 105 | + | 9 × 104 | + | 2 × 103 |
3.456 = 3.000 + 400 + 50 + 6 = 3 x 103 + 4 x 102 + 5 x 10 + 6
AHORA, PRACTICA PINCHANDO EN ESTAS ACTIVIDADES
  REPASO  |
6.- PROBLEMAS: RESOLVER PASO A PASO
1º Que nos quede claro qué nos pide el problema.
2º Seleccionar los datos que necesitamos.
3º Identificar las operaciones que debemos hacer primero.
CÁLCULO MENTAL
Sumar números de tres cifras.
456 + 238 = 674
400 + 200 = 600
50 + 30 = 80
6 + 8 = 14


























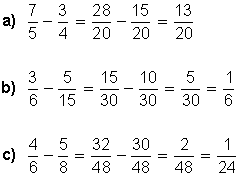





















![Operaciones combinadas (4)[3][4]](https://miclaseenlanube.files.wordpress.com/2011/09/operaciones-combinadas-434.jpg?w=470&h=341)
![Expresiones numéricas[3]](https://miclaseenlanube.files.wordpress.com/2011/09/expresiones-numricas3.jpg?w=470&h=342)
![Op. combinadas[3]](https://miclaseenlanube.files.wordpress.com/2011/09/op-combinadas3.jpg?w=470&h=341)




No hay comentarios:
Publicar un comentario